Le manoir récursif

2015/04/12 | Simon Rodriguez |
Table of Contents

Je me suis mis récemment en tête d’explorer un peu le domaine de la génération procédurale. Cet ensemble de techniques est revenu à la mode dans le monde du jeu vidéo ces dernières années. On pensera par exemple à Minecraft, Dwarf Fortress, No Man’s Sky,... L'idée générale est de confier une part de la réalisation des niveaux, de l'histoire, des textures, à un générateur pseudo-aléatoire qui suit certaines régles destinées à garantir la vraisemblance et la cohérence du tout. Selon les types de jeu, l'équilibre entre contenu généré à la main et contenu (plus ou moins aléatoire) varie. Dans le passé, la génération procédurale permettait de proposer des jeux riches en contenu malgré les limitations de l'époque en terme de stockage et de puissance de calcul. Ainsi Elite, sorti en 1984, proposait par exemple plus de 2000 systèmes solaires explorables tout en ne pesant que 20Ko. De nos jours, elle apporte une rejouabilité, la promesse d'environnements [1] plus variés, plus originaux et plus grands.

J'avais envie de comprendre comment générer aléatoirement des bâtiments, avec une répartition de couloirs, pièces, portes et fenêtres. La génération procédurale est souvent associée à la création d'éléments naturels, de par leurs structures fractales et chaotiques. Mais la production de créations humaines, comme des objets [2] ou des bâtiments est aussi utilisée, dans de nombreux RPGs notamment.

A terme l'idée serait de recréer un manoir, une vaste demeure avec de multiple recoins, des pièces par dizaines, meublées différement, et où se cacheraient des énigmes et des éléments issus de l'histoire du manoir. L'inspiration vient majoritairement de Gone Home (2013) et de Safecracker (2006), deux jeux qui ont en commun la pure exploration d'une vaste demeure déserte [3].

Mais comment faire ?

La première étape est de créer le plan du bâtiment, et de le peupler de pièces. Pour ce faire, on a besoin d'un algorithme de génération de pièces qui respecte certaines conditions :

Le dispositif le plus adapté semble alors être l'utilisation d'arbres binaires. Cette structure de données abstraite reproduit l'idée d'arbre généalogique : un arbre comporte une racine (un noeud), et deux branches (les sous-arbres), eux-mêmes composés d'un noeud et de deux sous-arbres, etc. jusqu'à ce qu'on arrive aux feuilles (des arbres dont les deux sous arbres sont vides). Les arbres se prêtent bien à des raisonnements récursifs, et c'est ce que nous allons faire ici : nous allons créer une arborescence de pièces emboîtées les unes dans les autres. Notre arbre, construit récursivement en partant de la racine (parcours descendant dans les branches) aura ainsi pour noeuds des pièces, dont les sous-arbres contiendront l'arborescence des pièces incluses dans la pièce qui tient lieu de noeud. Les feuilles de l'arbre seront les pièces finales. En procédant par subdivisions d'une grande pièce initiale, on sera ainsi sûr de peupler notre demeure en respectant les trois points ci-dessus.

Un exemple sera plus parlant

On commence avec un rectangle, définissant le corps de la demeure, qui contiendra plusieurs pièces et couloirs.

On ajoute des couloirs, selon une disposition tirée au hasard parmi un ensemble de d'agencements prédéfinis. Les couloirs définissent des super-pièces, ici au nombre de 3, qui contiendront des pièces et aucun couloir.
Pour chaque super-pièce, on sélectionne aléatoirement une orientation (horizontale/verticale) et un pourcentage, qui vont définir un point sur l'un des côtés de la super-pièce. Le tirage du pourcentage ne suit pas la loi uniforme, mais tend à privilégier des positions proches du milieu de la longueur du mur (en utilsiant une gaussienne). De la même façon, l'orientation tient compte du ratio de la super-pièce, pour éviter de se retrouver avec un mur créant deux pièces trop étroites.
Le point étant sélectionné, on trace le mur selon l'orientation choisie. On définit ainsi deux sous-super-pièces.
Selon leur taille, chaque sous-super-pièce a des chances de devenir une pièce à part entière. Ceci permet d'éviter de se retrouver avec un arbre binaire dont toutes les feuilles seraient à la même profondeur. Cependant, ici, ce n'est pas le cas.
Alors, pour chaque sous-super-pièce, on répète le processus de tirage d'un point et placement d'un mur (comme pour la super-pièce, vous suivez ?). On commence par tirer des points, avec des positions et orientations qui peuvent varier...
..., puis on trace les murs correspondants...
... et on obtient ainsi un nouveau niveau de pseudo-pièces, dont certaines peuvent devenir des pièces, là où les autres resteront des super-pièces sur lesquelles on rappliquera l'algorithme.
On répète ceci jusqu'à ce qu'on atteigne un des critères d'arrêt, à savoir une taille de pièce trop petite, ou une profondeur limite de l'arbre (passée en paramètre). En réalité, cette récursion s'applique sur chaque super-pièce simultanément.
On ajoute ensuite des ailes au manoir, disposées de façon à faire face aux extrémités des différents couloirs s'il y en a, et de manière aléatoire sinon. Ici, pour simplifier, les ailes ne comportent pas de couloirs, et chacune ne contient donc qu'une seule super-pièce.
Chaque super-pièce est remplie selon le même algorithme, en s'assurant que les couloirs ne débouchent pas sur une jonction de murs entre deux pièces. On a ainsi toutes les pièces de notre belle demeure !
Les portes peuvent être alors ajoutées. Pour chaque pièce P0 , on liste les pièces (et couloirs) P1,P2,...,PN qui lui sont adjacentes. Pour chaque Pi (i∈[1,N]), on vérifie s'il existe déjà une porte la reliant à P0 : si oui on ne rajoute pas de porte. Dans le cas contraire, plus P0 et Pi comportent de portes déjà existantes, moins il y a de chances qu'une nouvelle porte soit créée. Ceci permet d'éviter que toutes les pièces adjacentes soient toujours reliées entre elles, ce qui serait moins réaliste. Un tirage est donc réalisé avec une distribution pondérée selon le nombre total de portes de P0 et Pi. Si le tirage est positif, on ajoutera effectivement la porte entre les deux pièces. Sinon, on passe aux pièces suivantes.
La manière dont fonctionne l'algorithme peut causer des artefacts, sous la forme de pièces qui ne sont dotées d'aucune porte. Ce n'est pas un problème, tout manoir qui se respecte a des pièces cachées, des passages secrets et des réduits murés, témoins de l'indicible passé de la demeure. On note donc ces pièces comme non accessibles et on les masquent.
Ne reste plus qu'à ajouter la ou les portes vers l'extérieur, en s'alignant sur les couloirs.
Et voilà, notre demeure est prête. En réalité, rien n'a pour le moment été tracé, tout est stocké sous la forme d'un graphe gardant trace de toutes les pièces, les portes et couloirs, les dimensions et positions de chaque élément,...

Premières représentations

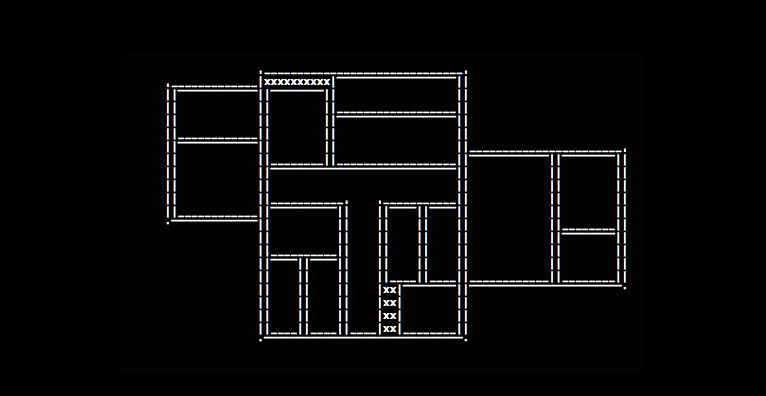
Ayant désormais construit le manoir sous forme d'une structure de données, il est interessant de le représenter visuellement. En réalité, cet affichage a été implémenté pendant le développement de la partie génération, pour pouvoir facilement débugger et visualiser le résultat d'une exécution du programme.

Il a été progressivement raffiné, passant d'une représentation ASCII à un rendu utilisant des sprites, gagnant en détail lorsque j'ajoutais des éléments (les portes par exemple). La représentation en 2D passe par la génération d'une matrice, où pour chaque case on spécifie le type d'image (tile) qui doit être chargée, pour afficher un mur droit, un angle, une jonction,... On effectue ainsi une projection, qui exige de parcourir l'ensemble de la structure représentant le bâtiment pour la traduire sous forme d'une carte.

Cette logique est plus difficile a appliquer pour passer à une représentation en trois dimensions : créer des tiles 3D impliquent de gérer correctement leurs raccordement et superposition (en évitant notamment le Z-fighting). Plus d'objets présents dans la scène implique plus de données à traiter, plus de draw calls, plus de difficultés pour gérer les textures. Bien entendu, certains de ces problèmes ont des solutions plus ou moins simples à mettre en place, et on parle ici d'au plus quelques centaines de sprites, rien de trop lourd. Mais dans l'optique d'enrichir et embellir les scènes par la suite (textures, meubles, éclairages), autant améliorer cette partie d'emblée.

La solution que j'ai choisie pour le moment est de génerer un tracé vectoriel des pièces de la demeure, et de l'extruder pour former un unique objet regroupant tous les murs. Cette méthode a le mérite d'être simple et de ne générer qu'un seul objet.
Par la suite il me faudra probablement trouver une méthode pour gérer chaque pièce séparément, afin de charger des textures et objets spécifiques pour chacune. Puis ajouter d'autres détails pour conférer à chaque manoir une atmosphère particulière, une histoire, des énigmes, des secrets. Implémenter un algorithme de placement de meubles, tel celui présenté ici serait probablement la prochaine étape, après un travail sur la modélisation des portes et des textures spécifiques à chaque pièce.

Sources

  1. et de créatures, pour Spore par exemple. ↩

  2. dans les jeux vidéo, on pourra penser à Borderlands 2 dans une certaine mesure ↩

  3. dans le premier cas pour comprendre ce qui est arrivée à notre famille pendant une longue absence, dans l'autre pour retrouver le testament du richissime propriétaire du manoir. ↩

  4. même si SceneKit manque de ressources en ligne : peu d'exemples complexes sont disponibles en dehors des études de cas officielles. ↩